High Dimensional Fixed Effects with Rossman Sales Data

Intro

This tutorial demonstrates how to create models with high dimensional fixed effects using glum. Using tabmat, we can pass categorical variables with a large range of values. glum and tabmat will handle the creation of the one-hot-encoded design matrix.

In some real-world problems, we have used millions of categories. This would be impossible with a dense matrix. General-purpose sparse matrices like compressed sparse row (CSR) matrices help but still leave a lot on the table. For a categorical matrix, we know that each row has only a single non-zero value and that value is 1. These optimizations are implemented in tabmat.CategoricalMatrix.

Background

For this tutorial, we will be predicting sales for the European drug store chain Rossman. Specifically, we are tasked with predicting daily sales for future dates. Ideally, we want a model that can capture the many factors that influence stores sales – promotions, competition, school, holidays, seasonality, etc. As a baseline, we will start with a simple model that only uses a few basic predictors. Then, we will fit a model with a large number of fixed effects. For both models, we will use OLS with L2 regularization.

We will use a gamma distribution for our model. This choice is motivated by two main factors. First, our target variable, sales, is a positive real number, which matches the support of the gamma distribution. Second, it is expected that factors influencing sales are multiplicative rather than additive, which is better captured with a gamma regression than say, OLS.

Note: a few parts of this tutorial utilize local helper functions outside this notebook. If you wish to run the notebook on your own, you can find the rest of the code here.

Table of Contents

• 1. Data Loading and Feature Engineering

• 2. Fit Baseline GLM

• 3. GLM with High Dimensional Fixed Effects

• 4. Plot Results

import os
from pathlib import Path

import altair as alt
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from dask_ml.impute import SimpleImputer
from dask_ml.preprocessing import Categorizer
from glum import GeneralizedLinearRegressor
from sklearn.pipeline import Pipeline

from feature_engineering import apply_all_transformations
from process_data import load_test, load_train, process_data

import sys
sys.path.append("../")
from metrics import root_mean_squared_percentage_error

pd.set_option("display.float_format", lambda x: "%.3f" % x)
pd.set_option('display.max_columns', None)
alt.data_transformers.enable("json")  # to allow for large plots

DataTransformerRegistry.enable('json')

1. Data loading and feature engineering

back to table of contents

We start by loading in the raw data. If you have not yet processed the raw data, it will be done below. (Initial processing consists of some basic cleaning and renaming of columns.

Note: if you wish to run this notebook on your own, and have not done so already, please download the data from the Rossman Kaggle Challenge. This tutorial expects that it in a folder named “raw_data” under the same directory as the notebook.

1.1 Load

if not all(Path(p).exists() for p in ["raw_data/train.csv", "raw_data/test.csv", "raw_data/store.csv"]):
    raise Exception("Please download raw data into 'raw_data' folder")

if not all(Path(p).exists() for p in ["processed_data/train.parquet", "processed_data/test.parquet"]):
    "Processed data not found. Processing data from raw data..."
    process_data()
    "Done"

df = load_train().sort_values(["store", "date"])
df = df.iloc[:int(.1*len(df))]
df.head()

	store	day_of_week	date	sales	customers	open	promo	state_holiday	school_holiday	year	month	store_type	assortment	competition_distance	competition_open_since_month	competition_open_since_year	promo2	promo2_since_week	promo2_since_year	promo_interval
1016095	1	2	2013-01-01	0	0	False	0	a	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None
1014980	1	3	2013-01-02	5530	668	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None
1013865	1	4	2013-01-03	4327	578	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None
1012750	1	5	2013-01-04	4486	619	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None
1011635	1	6	2013-01-05	4997	635	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None

1.2 Feature engineering

As mentioned earlier, we want our model to incorporate many factors that could influence store sales. We create a number of fixed effects to capture this information. These include fixed effects for:

• A certain number days before a school or state holiday

• A certain number days after a school or state holiday

• A certain number days before a promo

• A certain number days after a promo

• A certain number days before the store is open or closed

• A certain number days after the store is open or closed

• Each month for each store

• Each year for each store

• Each day of the week for each store

We also do several other transformations like computing the z score to eliminate outliers (in the next step)

df = apply_all_transformations(df)
df.head()

	store	day_of_week	date	sales	customers	open	promo	state_holiday	school_holiday	year	month	store_type	assortment	competition_distance	competition_open_since_month	competition_open_since_year	promo2	promo2_since_week	promo2_since_year	promo_interval	age_quantile	competition_open	count	open_lag_1	open_lag_2	open_lag_3	open_lead_1	open_lead_2	open_lead_3	promo_lag_1	promo_lag_2	promo_lag_3	promo_lead_1	promo_lead_2	promo_lead_3	school_holiday_lag_1	school_holiday_lag_2	school_holiday_lag_3	school_holiday_lead_1	school_holiday_lead_2	school_holiday_lead_3	state_holiday_lag_1	state_holiday_lag_2	state_holiday_lag_3	state_holiday_lead_1	state_holiday_lead_2	state_holiday_lead_3	store_day_of_week	store_month	store_school_holiday	store_state_holiday	store_year	zscore
1016095	1	2	2013-01-01	0	0	False	0	a	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None	-1	1.000	0	1.0	1.0	1.0	True	True	True	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	1.000	1.000	1.000	0	0	0	0	0	0	1_2	1_1	1_1	1_True	1_2013	NaN
1014980	1	3	2013-01-02	5530	668	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None	-1	1.000	1	False	1.0	1.0	True	True	True	0.000	0.000	0.000	0.000	0.000	0.000	1.000	0.000	0.000	1.000	1.000	1.000	a	0	0	0	0	0	1_3	1_1	1_1	1_False	1_2013	NaN
1013865	1	4	2013-01-03	4327	578	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None	-1	1.000	2	True	False	1.0	True	True	False	0.000	0.000	0.000	0.000	0.000	0.000	1.000	1.000	0.000	1.000	1.000	1.000	0	a	0	0	0	0	1_4	1_1	1_1	1_False	1_2013	NaN
1012750	1	5	2013-01-04	4486	619	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None	-1	1.000	3	True	True	False	True	False	True	0.000	0.000	0.000	0.000	0.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0	0	a	0	0	0	1_5	1_1	1_1	1_False	1_2013	NaN
1011635	1	6	2013-01-05	4997	635	True	0	0	1	2013	1	c	a	1270.000	9.000	2008.000	0	NaN	NaN	None	-1	1.000	4	True	True	True	False	True	True	0.000	0.000	0.000	0.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0	0	0	0	0	0	1_6	1_1	1_1	1_False	1_2013	NaN

1.3 Train vs. validation selection

Lastly, we split our data into training and validation sets. Kaggle provides a test set for the Rossman challenge, but it does not directly include outcome data (sales), so we do not use it for our tutorial. Instead, we simulate predicting future sales by taking the last 5 months of our training data as our validation set.

validation_window = [pd.to_datetime("2015-03-15"), pd.to_datetime("2015-07-31")]
select_train = (df["sales"].gt(0) & df["date"].lt(validation_window[0]) & df["zscore"].abs().lt(5)).to_numpy()

select_val = (
    df["sales"].gt(0)
    & df["date"].ge(validation_window[0])
    & df["date"].lt(validation_window[1])
).to_numpy()


(select_train.sum(), select_val.sum())

(57876, 12502)

2. Fit baseline GLM

back to table of contents

We start with a simple model that uses only year, month, day of the week, and store as predictors. Even with these variables alone, we should still be able to capture a lot of valuable information. Year can capture overall sales trends, month can capture seasonality, week day can capture the variation in sales across the week, and store can capture locality. We will treat these all as categorical variables.

With the GeneralizedLinearRegressor() class, we can pass in pandas.Categorical variables directly without having to encode them ourselves. This is convenient, especially when we start adding more fixed effects. But it is very important that the categories are aligned between calls to fit and predict. One way of achieving this alignment is with a dask_ml.preprocessing.Categorizer. Note, however, that the Categorizer class fails to enforce category alignment if the input column is already a categorical data type.

You can reference the pandas documentation on Categoricals to learn more about how these data types work.

baseline_features = ["year", "month", "day_of_week", "store"]
baseline_categorizer = Categorizer(columns=baseline_features)
baseline_glm = GeneralizedLinearRegressor(
    family="gamma",
    scale_predictors=True,
    l1_ratio=0.0,
    alphas=1e-1,
)

Fit the model making sure to process the data frame with the Categorizer first and inspect the coefficients.

baseline_glm.fit(
    baseline_categorizer.fit_transform(df[select_train][baseline_features]),
    df.loc[select_train, "sales"]
)

pd.DataFrame(
    {'coefficient': np.concatenate(([baseline_glm.intercept_], baseline_glm.coef_))},
    index=['intercept'] + baseline_glm.feature_names_
).T

	intercept	year__2013	year__2014	year__2015	month__1	month__2	month__3	month__4	month__5	month__6	month__7	month__8	month__9	month__10	month__11	month__12	day_of_week__1	day_of_week__2	day_of_week__3	day_of_week__4	day_of_week__5	day_of_week__6	day_of_week__7	store__1	store__2	store__3	store__4	store__5	store__6	store__7	store__8	store__9	store__10	store__11	store__12	store__13	store__14	store__15	store__16	store__17	store__18	store__19	store__20	store__21	store__22	store__23	store__24	store__25	store__26	store__27	store__28	store__29	store__30	store__31	store__32	store__33	store__34	store__35	store__36	store__37	store__38	store__39	store__40	store__41	store__42	store__43	store__44	store__45	store__46	store__47	store__48	store__49	store__50	store__51	store__52	store__53	store__54	store__55	store__56	store__57	store__58	store__59	store__60	store__61	store__62	store__63	store__64	store__65	store__66	store__67	store__68	store__69	store__70	store__71	store__72	store__73	store__74	store__75	store__76	store__77	store__78	store__79	store__80	store__81	store__82	store__83	store__84	store__85	store__86	store__87	store__88	store__89	store__90	store__91	store__92	store__93	store__94	store__95	store__96	store__97	store__98	store__99	store__100	store__101	store__102	store__103	store__104	store__105	store__106	store__107	store__108	store__109	store__110	store__111	store__112
coefficient	8.781	-0.010	0.008	0.003	-0.015	-0.021	-0.019	0.020	0.008	-0.006	-0.002	-0.023	-0.034	-0.030	0.022	0.116	0.098	0.010	-0.014	-0.014	0.017	-0.100	0.285	-0.156	-0.136	0.024	0.202	-0.161	-0.087	0.158	-0.094	0.002	-0.081	0.110	0.074	-0.126	-0.088	0.009	0.082	-0.020	0.001	-0.008	0.085	-0.088	-0.178	-0.088	0.183	0.274	0.008	0.192	-0.098	0.059	-0.101	-0.051	-0.225	0.125	0.102	0.198	0.185	0.046	-0.048	-0.153	-0.128	-0.085	0.234	0.017	-0.086	-0.101	-0.094	0.039	-0.243	0.058	-0.208	0.012	0.079	-0.109	0.099	-0.180	0.047	0.259	-0.017	-0.091	0.102	-0.149	-0.009	0.034	0.251	-0.122	-0.035	0.086	0.081	0.190	0.002	0.171	-0.189	-0.173	-0.023	-0.038	0.172	0.077	-0.266	-0.091	0.077	0.038	0.163	-0.248	0.369	0.019	-0.155	-0.060	-0.048	-0.047	0.130	-0.059	-0.047	-0.052	0.038	0.084	-0.121	0.007	-0.119	-0.111	0.108	0.069	0.038	-0.171	0.233	-0.175	0.136	0.058	0.284	-0.006	-0.174	0.018	-0.039

And let’s predict for our test set with the caveat that we will predict 0 for days when the stores are closed!

df.loc[lambda x: x["open"], "predicted_sales_baseline"] = baseline_glm.predict(
    baseline_categorizer.fit_transform(df.loc[lambda x: x["open"]][baseline_features])
)

df["predicted_sales_baseline"] = df["predicted_sales_baseline"].fillna(0)
df["predicted_sales_baseline"] = df["predicted_sales_baseline"]

We use root mean squared percentage error (RMSPE) as our performance metric. (Useful for thinking about error relative to total sales of each store).

train_err = root_mean_squared_percentage_error(
    df.loc[select_train, "sales"], df.loc[select_train, "predicted_sales_baseline"]
)
val_err = root_mean_squared_percentage_error(
    df.loc[select_val, "sales"], df.loc[select_val, "predicted_sales_baseline"]
)
print(f'Training Error: {round(train_err, 2)}%')
print(f'Validation Error: {round(val_err, 2)}%')

Training Error: 27.96%
Validation Error: 29.57%

The results aren’t bad for a start, but we can do better :)

3. GLM with high dimensional fixed effects

back to table of contents

Now, we repeat a similar process to above, but, this time, we take advantage of the full range of categoricals we created in our data transformation step. Since we will create a very large number of fixed effects, we may run into cases where our validation data has categorical values not seen in our training data. In these cases, Dask-ML’s Categorizer will output null values when transforming the validation columns to the categoricals that were created on the training set. To fix this, we add Dask-ML’s SimpleImputer to our pipeline.

highdim_features = [
    "age_quantile",
    "competition_open",
    "open_lag_1",
    "open_lag_2",
    "open_lag_3",
    "open_lead_1",
    "open_lead_2",
    "open_lead_3",
    "promo_lag_1",
    "promo_lag_2",
    "promo_lag_3",
    "promo_lead_1",
    "promo_lead_2",
    "promo_lead_3",
    "promo",
    "school_holiday_lag_1",
    "school_holiday_lag_2",
    "school_holiday_lag_3",
    "school_holiday_lead_1",
    "school_holiday_lead_2",
    "school_holiday_lead_3",
    "school_holiday",
    "state_holiday_lag_1",
    "state_holiday_lag_2",
    "state_holiday_lag_3",
    "state_holiday_lead_1",
    "state_holiday_lead_2",
    "state_holiday_lead_3",
    "state_holiday",
    "store_day_of_week",
    "store_month",
    "store_school_holiday",
    "store_state_holiday",
    "store_year",
]
highdim_categorizer = Pipeline([
    ("categorize", Categorizer(columns=highdim_features)),
    ("impute", SimpleImputer(strategy="most_frequent"))
])
highdim_glm = GeneralizedLinearRegressor(
    family="gamma",
    scale_predictors=True,
    l1_ratio=0.0, # only ridge
    alpha=1e-1,
)

For reference, we output the total number of predictors after fitting the model. We can see that the number getting a bit larger, so we don’t print out the coefficients this time.

highdim_glm.fit(
    highdim_categorizer.fit_transform(df[select_train][highdim_features]),
    df.loc[select_train, "sales"]
)

print(f"Number of predictors: {len(highdim_glm.feature_names_)}")

Number of predictors: 2771

df.loc[lambda x: x["open"], "predicted_sales_highdim"] = highdim_glm.predict(
    highdim_categorizer.transform(df.loc[lambda x: x["open"]][highdim_features]),
)

df["predicted_sales_highdim"] = df["predicted_sales_highdim"].fillna(0)
df["predicted_sales_highdim"] = df["predicted_sales_highdim"]


train_err = root_mean_squared_percentage_error(
    df.loc[select_train, "sales"], df.loc[select_train, "predicted_sales_highdim"]
)
val_err = root_mean_squared_percentage_error(
    df.loc[select_val, "sales"], df.loc[select_val, "predicted_sales_highdim"]
)
print(f'Training Error: {round(train_err, 2)}%')
print(f'Validation Error: {round(val_err, 2)}%')

Training Error: 12.54%
Validation Error: 13.28%

From just the RMSPE, we can see a clear improvement from our baseline model.

4. Plot results

back to table of contents

Finally, to get a better look at our results, we make some plots.

sales_cols = ["sales", "predicted_sales_highdim", "predicted_sales_baseline"]

First, we plot true sales and the sales predictions from each model aggregated over month:

_, axs = plt.subplots(2, 1, figsize=(16, 16))

for i, select in enumerate([select_train, select_val]):
    ax = axs[i]
    df_plot_date = df[select].groupby(
        ["year", "month"]
    ).agg("sum")[sales_cols].reset_index()

    year_month_date = df_plot_date['month'].map(str)+ '-' + df_plot_date['year'].map(str)
    df_plot_date['year_month'] = pd.to_datetime(year_month_date, format='%m-%Y').dt.strftime('%m-%Y')
    df_plot_date.drop(columns= ["year", "month"], inplace=True)

    df_plot_date.plot(x="year_month", ax=ax)
    ax.set_xticks(range(len(df_plot_date)))
    ax.set_xticklabels(df_plot_date.year_month, rotation=45)
    ax.set_xlabel("date")
    ax.set_ylabel("Total sales")
    ax.grid(True, linestyle='-.')

axs[0].set_title("Training Results: Total Sales per Month")
axs[1].set_title("Validation Results: Total Sales per Month")
plt.show()

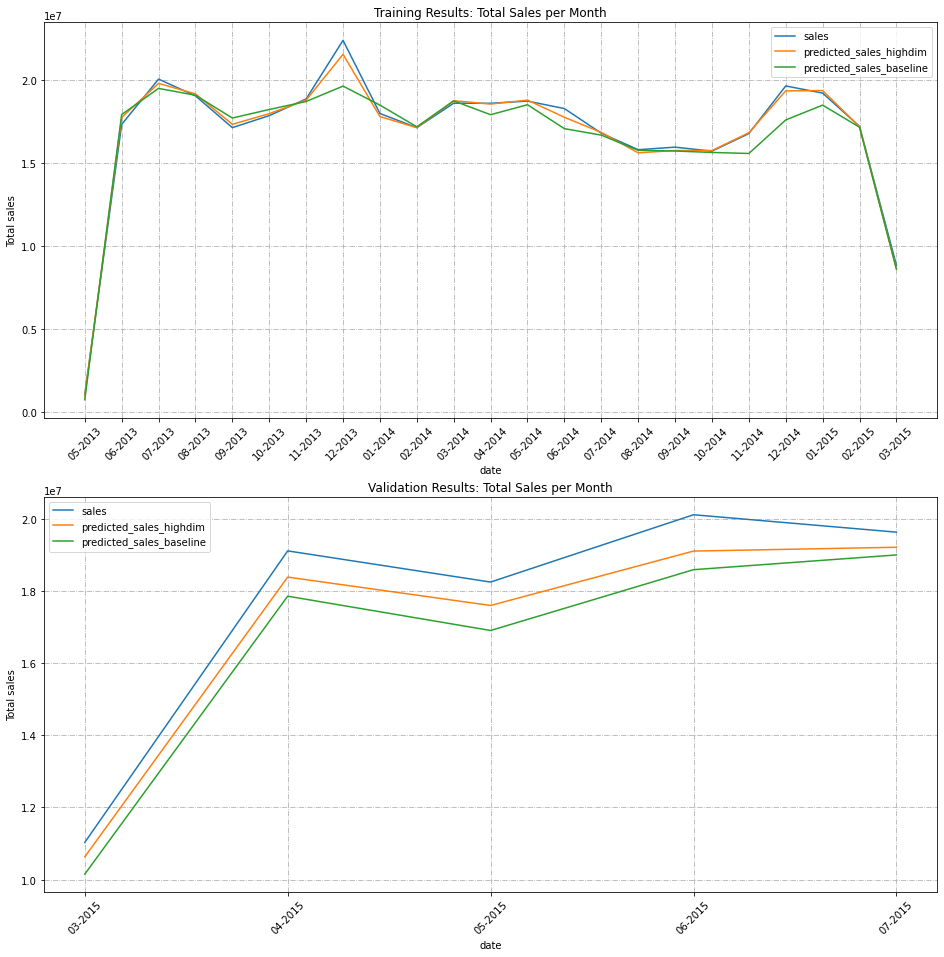
We can also look at aggregate sales for a subset of stores. We select the first 20 stores and plot in order of increasing sales.

_, axs = plt.subplots(2, 1, figsize=(14, 12))
for i, select in enumerate([select_train, select_val]):
    ax = axs[i]
    df_plot_store = df[select].groupby(
        ["store"]
    ).agg("sum")[sales_cols].reset_index()[:20].sort_values(by="sales")

    df_plot_store.plot.bar(x="store", ax=ax)
    ax.set_xlabel("Store")
    ax.set_ylabel("Total sales")

axs[0].set_title("Training Results: Total Sales by Store")
axs[1].set_title("Validation Results: Total Sales by Store")
plt.show()

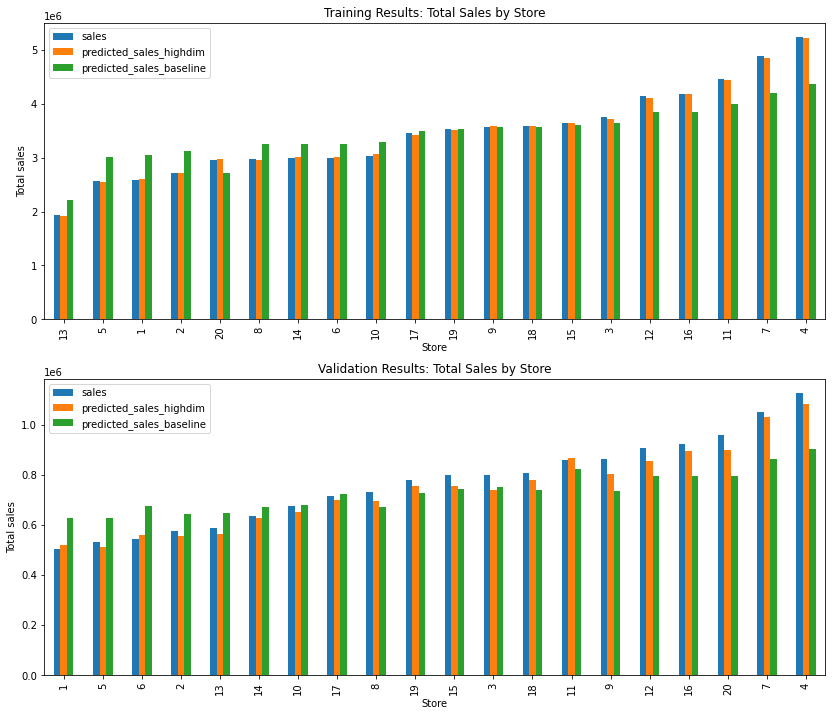
We can see that the high dimensional model is much better at capturing the variation between months and individual stores!